Iterative Solvers module

Detailed Description

This module aims to provide various iterative linear and non linear solver algorithms. It currently provides:

• a constrained conjugate gradient
• a Householder GMRES implementation
• an IDR(s) implementation
• a BiCGSTAB(L) implementation
• a DGMRES implementation
• a MINRES implementation
• a IDRSTABL implementation

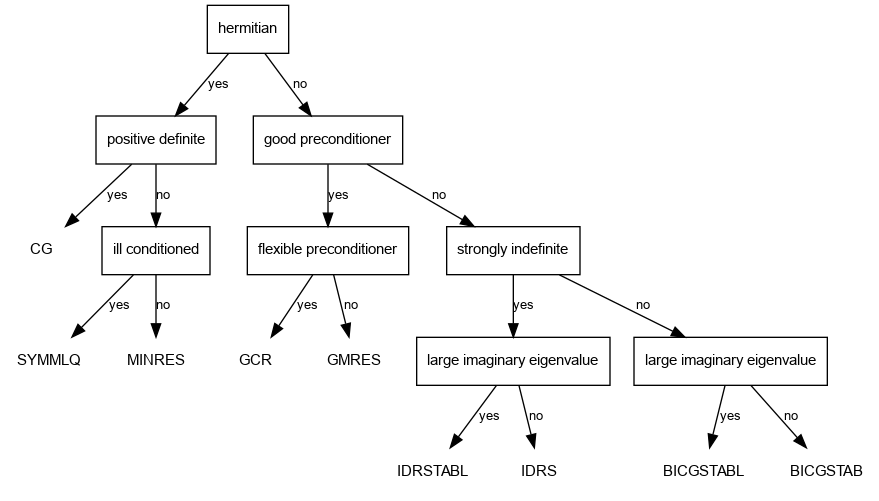
Choosing the best solver for solving A x = b depends a lot on the preconditioner chosen as well as the properties of A. The following flowchart might help you.

#include <unsupported/Eigen/IterativeSolvers>

Classes
class	Eigen::DGMRES< MatrixType_, Preconditioner_ >
	A Restarted GMRES with deflation. This class implements a modification of the GMRES solver for sparse linear systems. The basis is built with modified Gram-Schmidt. At each restart, a few approximated eigenvectors corresponding to the smallest eigenvalues are used to build a preconditioner for the next cycle. This preconditioner for deflation can be combined with any other preconditioner, the IncompleteLUT for instance. The preconditioner is applied at right of the matrix and the combination is multiplicative. More...
class	Eigen::GMRES< MatrixType_, Preconditioner_ >
	A GMRES solver for sparse square problems. More...
class	Eigen::IDRS< MatrixType_, Preconditioner_ >
	The Induced Dimension Reduction method (IDR(s)) is a short-recurrences Krylov method for sparse square problems. More...
class	Eigen::IDRSTABL< MatrixType_, Preconditioner_ >
	The IDR(s)STAB(l) is a combination of IDR(s) and BiCGSTAB(l). It is a short-recurrences Krylov method for sparse square problems. It can outperform both IDR(s) and BiCGSTAB(l). IDR(s)STAB(l) generally closely follows the optimal GMRES convergence in terms of the number of Matrix-Vector products. However, without the increasing cost per iteration of GMRES. IDR(s)STAB(l) is suitable for both indefinite systems and systems with complex eigenvalues. More...
class	Eigen::IterationController
	Controls the iterations of the iterative solvers. More...
class	Eigen::MINRES< MatrixType_, UpLo_, Preconditioner_ >
	A minimal residual solver for sparse symmetric problems. More...

Functions
template<typename TMatrix , typename CMatrix , typename VectorX , typename VectorB , typename VectorF >
void	Eigen::internal::constrained_cg (const TMatrix &A, const CMatrix &C, VectorX &x, const VectorB &b, const VectorF &f, IterationController &iter)
template<typename CMatrix , typename CINVMatrix >
void	Eigen::internal::pseudo_inverse (const CMatrix &C, CINVMatrix &CINV)

Function Documentation

constrained_cg()

template<typename TMatrix , typename CMatrix , typename VectorX , typename VectorB , typename VectorF >

void Eigen::internal::constrained_cg	(	const TMatrix &	A,
		const CMatrix &	C,
		VectorX &	x,
		const VectorB &	b,
		const VectorF &	f,
		IterationController &	iter
	)

Constrained conjugate gradient

Computes the minimum of \( 1/2((Ax).x) - bx \) under the constraint \( Cx \le f \)

pseudo_inverse()

template<typename CMatrix , typename CINVMatrix >

void Eigen::internal::pseudo_inverse	(	const CMatrix &	C,
		CINVMatrix &	CINV
	)

Compute the pseudo inverse of the non-square matrix C such that \( CINV = (C * C^T)^{-1} * C \) based on a conjugate gradient method.

This function is internally used by constrained_cg.